Die Lösungen unserer Übungsaufgaben erhaltet ihr, wenn ihr auf die folgenden Vorschaubilder klickt.
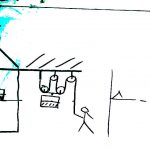


Der Pentaspastos
Die folgende Abbildung zeigt die Längen am Pentaspastos.
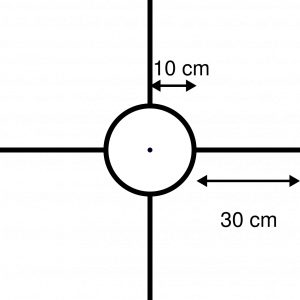
Man sieht, dass der Hebelarm der Hebel, an denen die Männer drehen, vier Mal so lang sind, wie der Hebel, an dem das Seil aufgewickelt wird. Die Zugkraft am Seil ist also vier Mal so groß wie die Kraft, mit der die Männer drehen ($2 \cdot \SI{150}N = \SI{300}N$). Also: $F_\text{Z} = 4 \cdot \SI{300}{N} = \SI{1200}N$.
Da der Flaschenzug 5 tragende Seile besitzt, darf ein daran hängendes Gewicht eine fünf Mal so große Gewichtskraft besitzen, wie die Kraft, mit der am Seil gezogen wird: $F_\text{G} = 5 \cdot F_\text{Z} = 5 \cdot \SI{1200}N = \SI{6000}N$. Das Gewicht darf also bis zu $\SI{600}{kg}$ schwer sein.