Aufgaben
Im Jahr 1972 erschien mit dem HP-35 der erste technisch-wissenschaftliche Taschenrechner bis dahin nutze man zum schnellen Rechnen den sogenannten Rechenschieber. Wie der funktioniert, erarbeitest du dir in den folgenden Aufgaben.
- Berechne die folgenden Terme. Vergleiche die Ergebnisse.
- $\lg 10$, $\lg 5$ und $\lg 50$
- $\log_3 7$, $\log_3 7$, $\log_3 21$
- Anhand der vorherigen Aufgabe kann man das Logarithmengesetz $$\log_c (a\cdot b) = \log_c (a) + \log_c (b)$$ erkannt haben, d. h. der Logarithmus eines Produkts ist die Summe der beiden Logarithmen. Diese Gesetzmäßigkeit kann man sich übrigens mithilfe der Potenzgesetze herleiten.
- Beim Rechenschieber wird diese Gesetzmäßigkeit genutzt, um Zahlen mithilfe der Addition von Strecken multiplizieren zu können. Stephan Mueller hat hierzu ein schönes Erklärvideo erstellt.
Ab jetzt hast du drei Möglichkeiten:- In Variante 1 lädst du dir einen Papierrechenschieber herunter, druckst ihn aus und bastelst ihn zusammen.
- Du nutzt einen Online-Rechenschieber.
- Schneide aus Papier verschiedene Rechtecke wie in der folgenden Abbildung aus. Das erste Rechteck erhält die Länge $\log_{1{,}2} 2$, das zweite die Länge $\log_{1{,}2} 3$, … das fünfundzwanzigste die Länge $\log_{1{,}2} 25$.
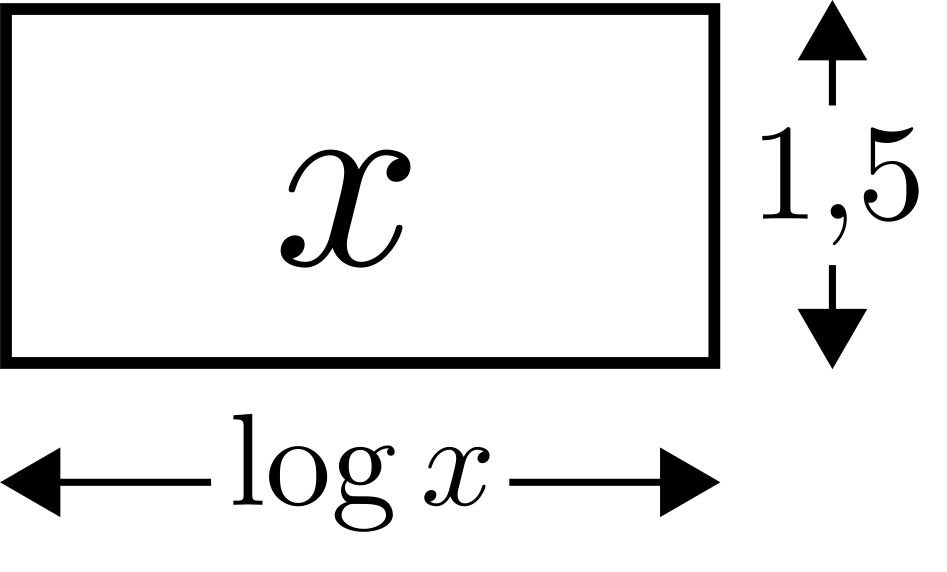
- Berechne die folgenden Produkte mithilfe des Rechenschiebers/deiner Rechtecke:
- $5 \cdot 4$
- $7 \cdot 9$
- $4{,}7 \cdot 2{,8}$
- Drehe ein kurzes Video, in dem du erklärst, wie man mit dem Rechenschieber zwei Zahlen multipliziert. Alternative: Erstelle mithilfe der ausgeschnittenen Logarithmenstücke eine kurze Anleitung, mit der du erklärst, wie man zwei Zahlen mithilfe dieser Stücke schnell multiplizieren kann.
Hilfe
Für weitere Hilfe könnt ihr euch gerne bei mir melden.
In der Wikipedia gibt es auch eine Erklärung.
Abgabe der Lösungen
Lade deine Lösung von Aufgabe 5 bis Freitag (03.04.) um 12:00 Uhr unter diesem Link hoch. Vergiss nicht, deine Lösung zu beschriften oder die Datei korrekt zu benennen.
