Bitte bearbeiten Sie zur Vorbereitung auf die morgige Videokonferenz die folgenden Aufgaben und schauen Sie sich kurz noch einmal an, wie man lineare Gleichungssysteme löst.
Einstieg – Funktionsterm gesucht
Im folgenden Bild sehen Sie den Graphen der Funktion $f$, in dem bereits charakteristische Punkte und eine Tangente eingezeichnet sind. Unser Ziel soll es später sein, den Funktionsterm zu berechnen.
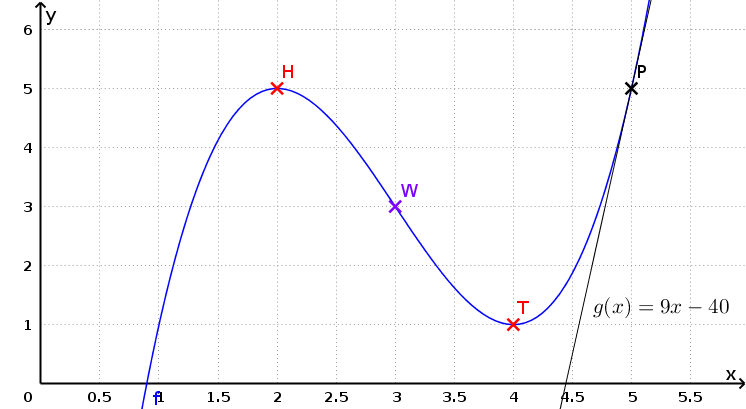
Ganz einfach lassen sich hier die Koordinaten der Punkte angeben. Das sparen wir uns hier mal. Man kann nämlich auch noch ganz andere Eigenschaften der Funktion angeben:
Der Graph von $f$
- besitzt an den Stellen 2 und 4 Extrempunkte,
- hat an der Stelle 3 einen Wendepunkt und
- besitzt an der Stelle 5 eine Wendetangente mit Steigung 9.
Diese Eigenschaften lassen sich in Gleichungen übersetzen, die wir später zum Rekonstruieren des Funktionsterms nutzen können.
- Hochpunkt: $f'(2) = 0$
- Tiefpunkt: $f'(4) = 0$
- Wendepunkt: $f“(3) = 0$
- Tangente $f'(5) = 9$
Aufgaben
Gegeben sind die beiden Graphen der Funktionen $f$ und $g$.
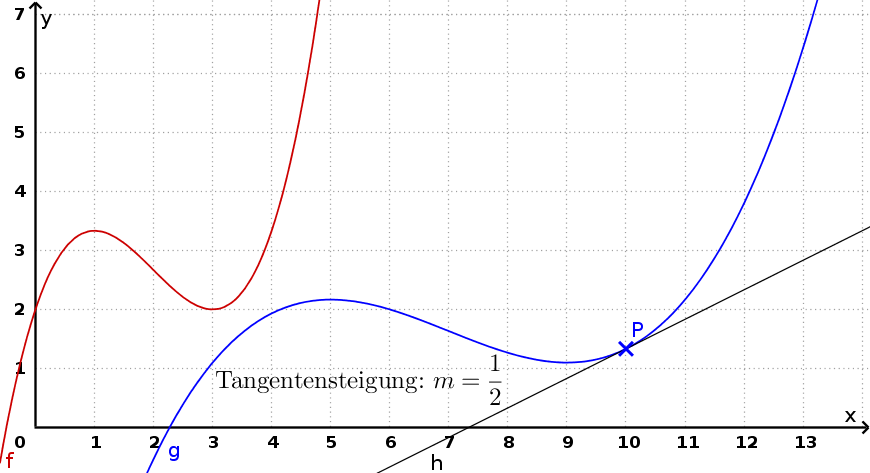
- Beschreiben Sie wie im Beispiel die Eigenschaften der Funktionsgraphen.
- Übersetzen Sie die Eigenschaften wie im Beispiel in Gleichungen.
Abgabe
Wir besprechen die Aufgabe morgen in der Videokonferenz. Sie dürfen gerne freiwillig Ihr Lösung vorher ins Schulportal hochladen. Wie das geht, sehen können Sie in einem von mir erstellten Erklärvideo sehen.
