Das von Ihnen erstellte Video können Sie hier hochladen. Das Passwort finden Sie auf Ihrem Arbeitsblatt.
Arbeitshefte
Klasse 6d
Liebe Eltern der Klasse 6d,
bitte besorgen Sie Ihrem Kind das zum Buch passende Arbeitsheft bis zum 30.08. Vorher nutzten wir noch das Heft aus der 5. Klasse.
Mathematik Einführungsphase
Lieber Schülerinnen und Schüler der Einführungsphase,
falls Sie noch Förderbedarf haben, so können Sie sich das Arbeitsheft zum Vertiefungskurs in NRW besorgen.
Mit diesem Heft können Sie selbstständig arbeiten. Sie können mich aber auch gerne bei Fragen nach dem Unterricht spontan ansprechen oder einen Termin mit mir vereinbaren.
Ph-E Hausaufgabe: Eigene Fragen zum Diagramm
Im Arbeitsmaterial finden Sie einen Link zu einer Seite, auf der Sie bitte Ihre Frage eintragen. Falls das nicht klappt, Schreiben Sie Ihre Frage doch bitte einfach in die Kommentare.
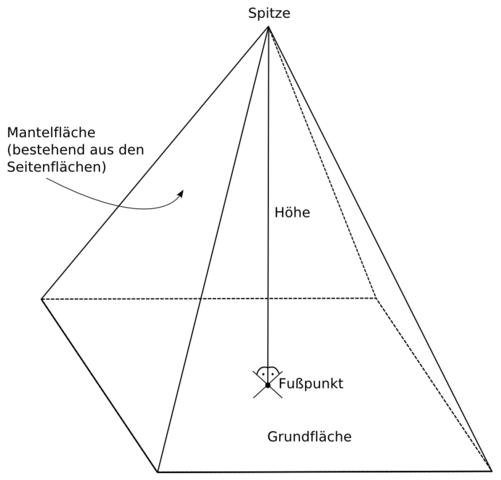
Berechnungen an einer Pyramide
Projektarbeiten Physik Einführungsphase
Mögliche Themen und die Bedingungen für die Projektarbeiten finden Sie hier. Bitte vereinbaren Sie einen Termin über die Terminverwaltung.
Lösung der Übungsaufgaben für die Lernkontrolle
Aufgabe 1
Aufgabe 1 haben wir in der Schule gemeinsam gelöst.
Aufgabe 2
Beim Winkel von $\ang{180}$ subtrahiert man die Kräfte voneinander. Es bleiben also $\SI{2}{N}$ übrig. Geht man so vor, wie im Bild, zeigt die Kraft nach links.
Aufgabe 3
a) Peter läuft bei $t=\SI{0}{s}$ bei 50 m los und erreicht nach 10 Sekunden den Zielort bei 100 m. Dort wartet er 10 Sekunden und läuft anschließend in die andere Richtung zurück. Nach insgesamt 60 Sekunden (40 Sekunden später) erreicht er den Punkt 0 Meter.
b) $v_1 = \frac{\Delta s}{\Delta t} = \frac{\SI{50}{m}}{\SI{10}{s}} = \SI[per-mode=fraction]{5}{\meter\per\second}$
$v_2 = \SI[per-mode=fraction]{0}{\meter\per\second}$
$v_3 = – \SI[per-mode=fraction]{2,5}{\meter\per\second}$
Aufgabe 4
a) $D = \frac{F}{\Delta s} = \frac{\SI{20}{N}}{\SI{70}{cm}} \approx \SI[per-mode=fraction]{0,29}{\newton\per\centi\meter}$
b)$\Delta s = \frac FD = \frac{ \SI{30}{N} }{ \SI[per-mode=fraction]{0,29}{\newton\per\centi\meter} } \approx \SI{103}{cm}$
Wenn man an die Feder ein Gewicht der Masse $\SI{3}{kg}$ hängt, verlängert sie sich auf $\SI{133}{cm}$
Beispielaufgaben Potenzrechnung
Eine Zusammenfassung der Potenzrechnung und Beispielaufgaben findet ihr in meinen neuen Wiki.
Fragen könnt ihr mir per E-Mail schicken, in die Kommentare schreiben oder in der neuen Frage- und Antwortrubrik stellen.
Rechnen mit Einheiten
Auf der verlinkten Webseite könnt ihr das Umrechnen von Einheiten üben.
LS 9, S. 68, Nr. 5
Hier wie gewünscht die Lösung zu Aufgabe 5(a) auf Seite 68. Ich habe jeweils nur die Formeln und das Ergebnis hingeschrieben. Die Fläche habe ich weggelassen. Falls ihr einen Fehler findet, dann meldet euch bitte.
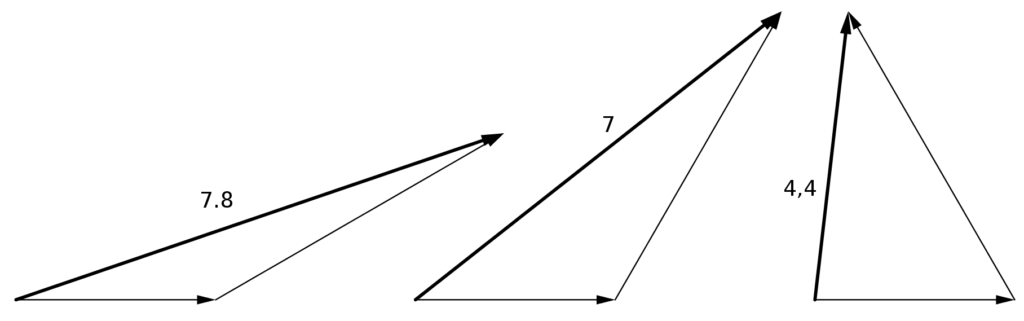
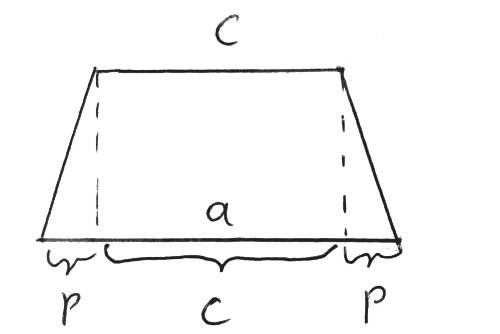
Die nicht benannte Seite des kleinen Dreiecks rechts nenne ich $p$. Dann ist $\tan\beta = \frac hp$. Also kann man $p \approx \num{2.38}$ ausrechnen. Mit dem Satz des Pythagoras $p^2 + h^2 = b^2$ hat man $b \approx \num{5,63}$ ($b = d$). $a$ hat man mit der Gleichung $ a = c + 2p = \num{8,26}$. Im Dreieck mit den Seiten $h,e$ und einem Teile von $a$ nutzt man den Satz des Pythagoras. Es gilt: $(c+p)^2 + h^2 = e^2$. Daraus errechnet man $e = \num{7,78}$. Es gilt außerdem $\tan{\alpha_1} = \frac h{c+p}$, womit man $\alpha_1 \approx \ang{39}$ berechnen kann. $\alpha_1$ und $\alpha_2$ ergeben zusammen den Winkel $\beta$, sodass $\alpha = \beta – \alpha_1 = \ang{16}$ beträgt.
Bei Aufgabenteil b) berechnet man zunächst $p$ mit $a = c + 2p$ und dann $h$ mit dem Satz des Pythagoras ($(c+p)^2 + h^2 = e^2$). Das Dreieck mit den Seiten $e, b$ und $h$ ist nicht unbedingt rechtwinklig!
Lösungen der Übungsaufgaben für die Arbeit
Eure Lösungen könnt ihr hier herunterladen. Sollte sich irgendwo ein Fehler eingeschlichen haben, könnt ihr gerne etwas in die Kommentare posten oder mir eine Mail schreiben.