Punktspiegelung und Punktsymmetrie
Diese Woche lernen wir, was Punktsymmetrie ist und erarbeiten uns, wie man Punkte und Figuren an einem Punkt spiegelt.
Test
Bevor du weitermachst hier noch ein kurzer Test zu dem, was wir bisher gemacht haben.
Punktsymmetrie
Die folgenden Figuren sind symmetrisch, besitzen jedoch keine Spiegelachse.
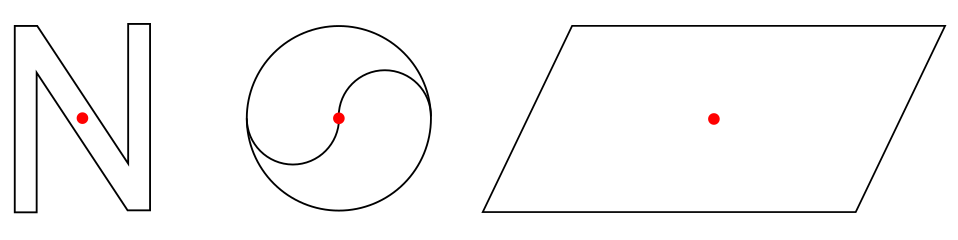
Auch Windräder sind (oft) punktsymmetrisch.

Punktsymmetrie überprüfen
Willst du überprüfen, ob eine Figur punktsymmetrisch ist, verbindet man wie im folgenden Bild zusammengehörige Punkte. Zeichne das Bild unter der Überschrift Punktsymmetrie in dein Regelheft.
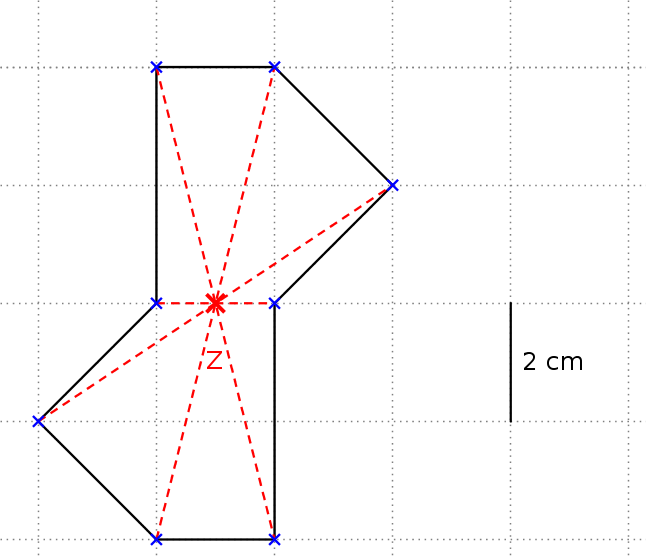
Die Figur ist punktsymmetrisch, da sich alle roten Strecken in einem Zentrum $Z$ (manchmal auch $S$ für Spiegelpunkt oder Symmetriepunkt) schneiden und der Punkt $Z$ die Strecken halbiert. Miss das nach.
Aufgaben
- Bearbeite auf S. 29 im Arbeitsheft die Nr. 2.
- Zeichne selbst drei punktsymmetrische Figuren.
Punktspiegelung
Wenn es eine Punktsymmetrie gibt, dann gibt es natürlich auch eine Punktspiegelung. Wie die funktioniert, erklärt Lehrerschmidt in einem Video. Zeichne die beiden Figuren aus dem Video unter der Überschrift Punktspiegelung in dein Regelheft. Darunter kommt dann die folgende Erklärung der Vorgehensweise:
- Verbinde jeden Punkt (z. B. $A$) mit dem Zentrum $Z$ und zeichne dabei mindestens die gleiche Länge darüber hinaus.
- Stich mit dem Zirkel in das Zentrum, stelle ihn so ein, dass die Bleistiftspitze im Punkt $A$ liegt und übertrage diese Länge auf die andere Seite der gerade eben gezeichneten Linie. Markiere diese Stelle. Dort ist der Bildpunkt $A’$. Alternativ kannst du auch die Länge mit dem Geodreieck messen und übertragen.
Aufgaben
- Im Buch auf S. 106 findest du in Nr. 10 verschiedene Figuren. Übertrage sie in dein Heft und spiegele sie jeweils am Zentrum $Z$. Hinweis: Du musst jedes Mal etwas Platz nach oben lassen.
- S. 106 Nr. 8.
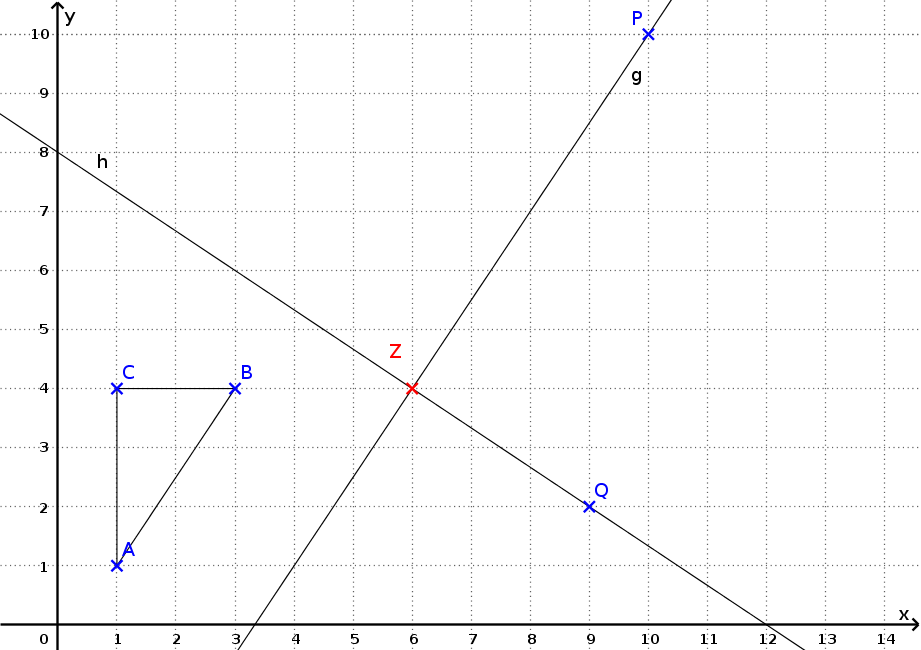
- Gegeben ist das Dreieck $ABC$ mit den Punkten $A( 1\mid1 )$, $B(3 \mid 4)$ und $C( 1\mid 4)$. Außerdem gibt es die Punkte $Z( 6\mid4 )$, $P( 10\mid10 )$ und $Q(9 \mid 2)$. Die Gerade $g$ geht durch die Punkte $Z$ und $P$, die Gerade $h$ geht durch die Punkte $Z$ und $Q$.
- Zeichne das Koordinatensystem zweimal in dein Heft.
- Spiegele das Dreieck $ABC$ im ersten Diagramm zunächst an der Geraden $h$ und das entstandene Bilddreieck anschließend an der Geraden $g$.
- Spiegele das Dreieck $ABC$ im zweiten Diagramm am Punkt $Z$.
- Beschreibe, was dir bei den beiden Ergebnissen auffällt.
Hier klicken für Hilfe zum Zeichnen des Koordinatensystems.
Lösung hochladen
Lade deine persönliche Lösung der Aufgaben zur Punktspiegelung (Aufgaben 3-5) bis Donnerstag, dem 14.05.2020 (20:00 Uhr) ins Schulportal hoch.
Unabhängig davon, welche Aufgabe hochgeladen werden soll, sollen natürlich möglichst alle Aufgaben bearbeitet werden.
Organisatorisches
Auch in dieser Woche gibt es eine Videosprechstunde, an der jeder freiwillig teilnehmen kann. Ihr könnt einen Termin unter Terminvereinbarung buchen.
